A New Paradigm for Exploiting Pre-trained Model Hubs

The Overlooked Scaling-up Number
In recent years, there has been a constant pursuit to build larger and larger models, since researchers observed that scaling up models brought significant improvement in language understanding [1]. The following figure (credit to this blog) shows that model size scales up exponentially every year. Large companies are in a hot arms race to win the title of "largest model to date".
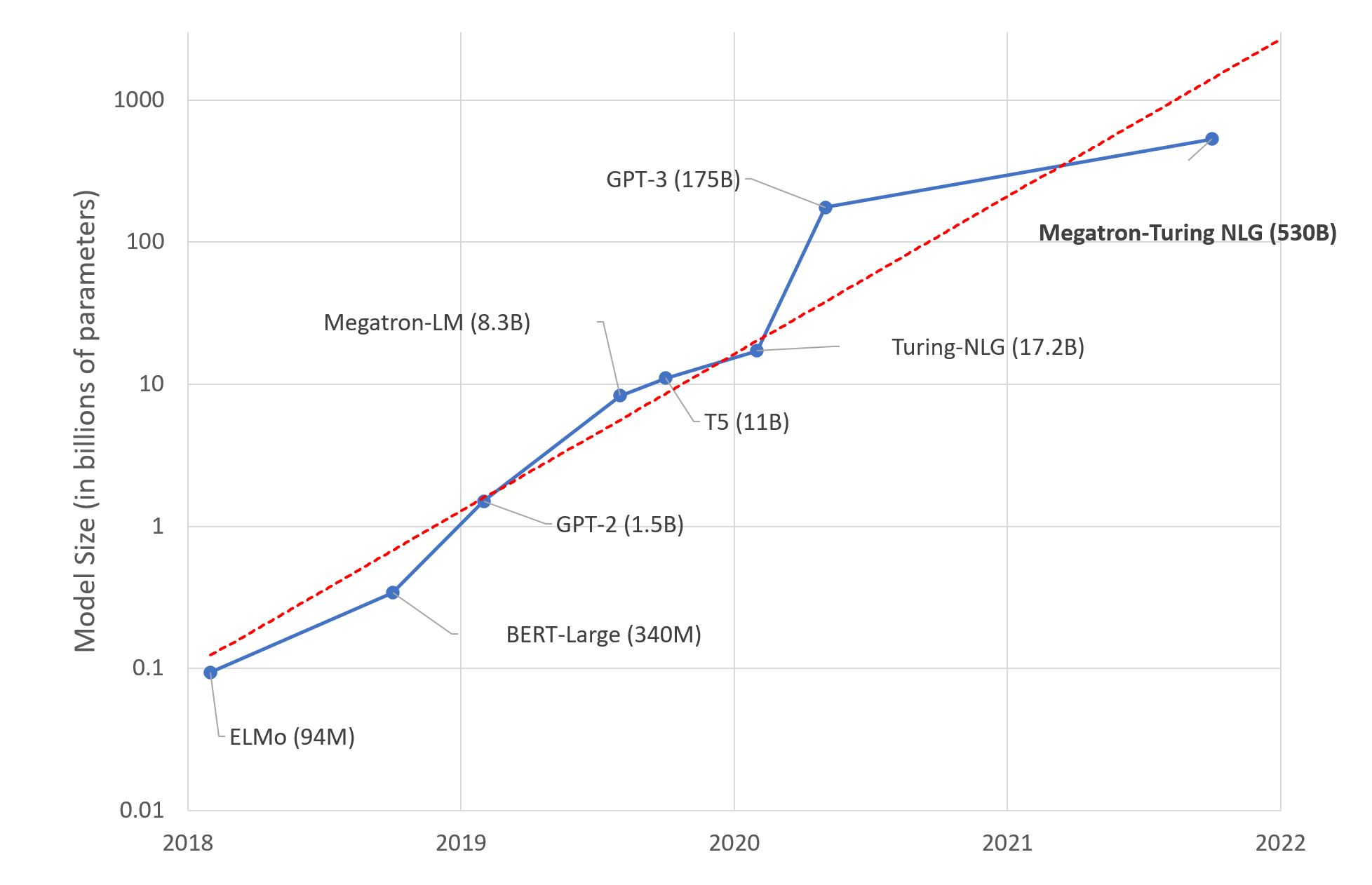
The scale of models in recent years (log scale y-axis).
It is often overlooked, however, that the number of public available models also scales up exponentially. The HuggingFace Models is a famous hub for hosting pre-trained models. From the upload history of every model, I calculate the number of new models every year, and plot the trend in the following figure. The figure clearly shows an exponentially increasing trend for the number of available pre-trained models.
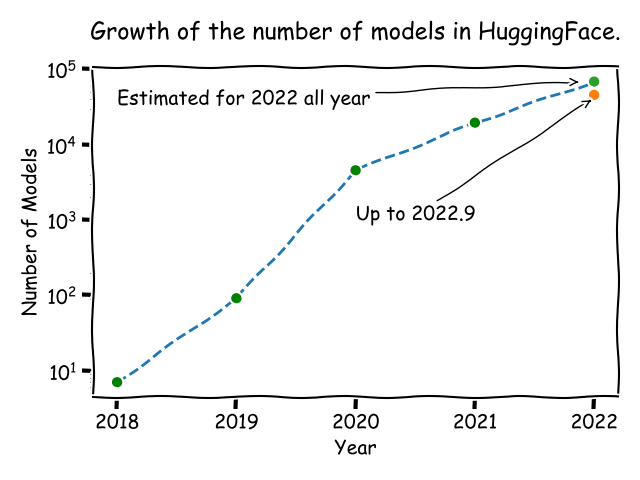
The growth of the number of models in HuggingFace.
The Popular But Under-exploited Model Hub
It is true that HuggingFace Models is very popular. Nevertheless, I find that the whole model hub is under-exploited, in terms of the number of models being used. The following figure is taken from my JMLR paper [2]. It analyzes the download count per month for all the pre-trained models in the HuggingFace Models. There are some obvious observations:
- Pre-trained models (PTMs) have become a cornerstone of deep learning. A single model hub has over 150 million downloads in just one month.
- The distribution of download count is extremely skewed. BERT contributes over a half. The top 10 models (except BERT) contribute less than a quarter. The top 1000 models (except the top 10) contribute less than a quarter.
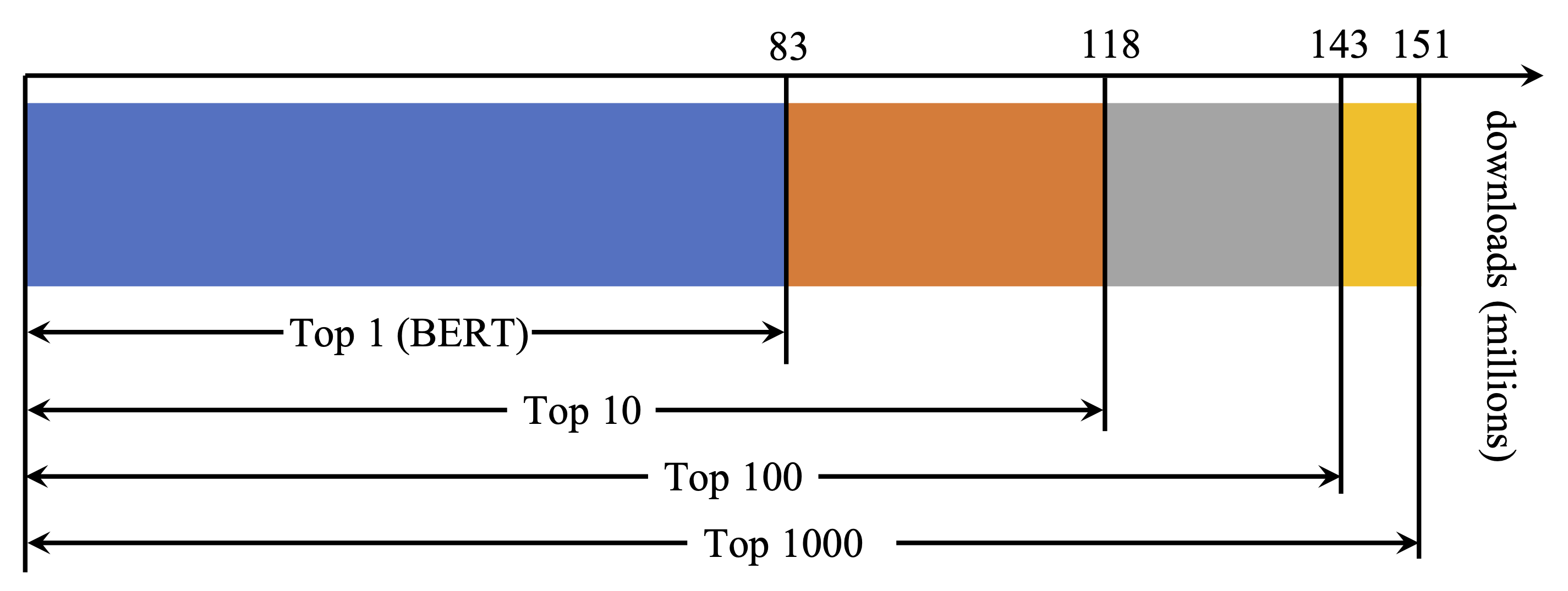
Monthly download statistics (in millions) for top popular models.
In its current state, the model hub looks like a large UGC community with abundant user-generated content. Due to the lack of a recommendation system for pre-trained models, however, practitioners just pick the most popular model and nobody cares about the rest models, resulting the dilemma that the model hub is popular but under-exploited.
A New Paradigm For Exploiting Model Hubs
The key to sufficiently exploiting model hubs is to take advantage of those under-exploited models. A good recommendation system should recommend content according to the user's preference, and so should a good paradigm for exploiting model hubs. In the last year, I worked hard on this problem and I want to share some of my thoughts here.
So far, I have made several analogies between recommendation systems and model hubs. It is intuitive for readers to understand the main idea, but technical details are different. To be specific, recommendation systems deal with "real users" and their goal is to predict user behavior, while model hubs deal with tasks and their goal is to solve a task with the help of pre-trained models.
The paradigm I propose in the paper [2] is to treat model hub as a service: a user comes with a task in the form of a dataset
- If the user has no preference for the model's architecture, just fine-tune the best-ranked model directly.
- If the user desires a specific model but it is not the best (e.g. a small model for fast inference): transfer top-K ranked models to the target model.
The paradigm is summarized in the following figure, and next I will elaborate on each step.
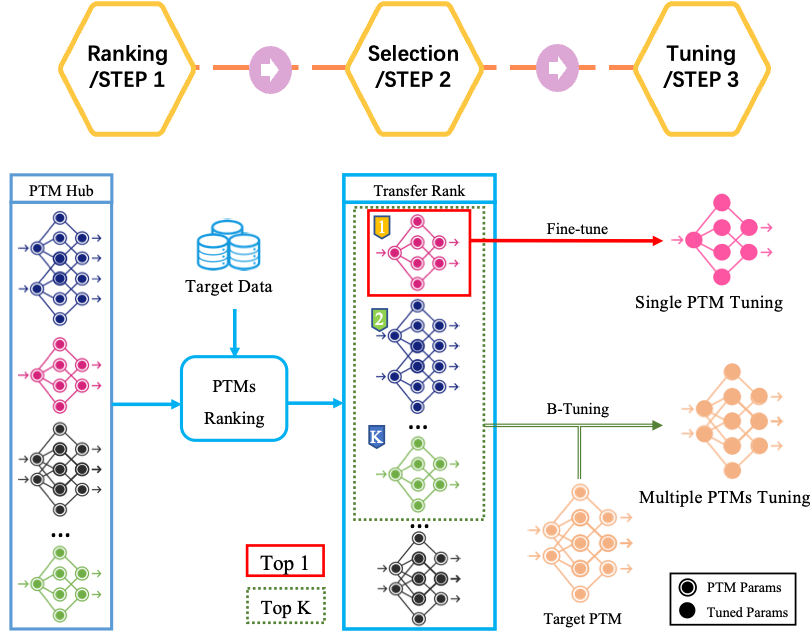
The "ranking and tuning" paradigm.
Ranking Pre-trained Models
The first thing is to predict the performance of a pre-trained model
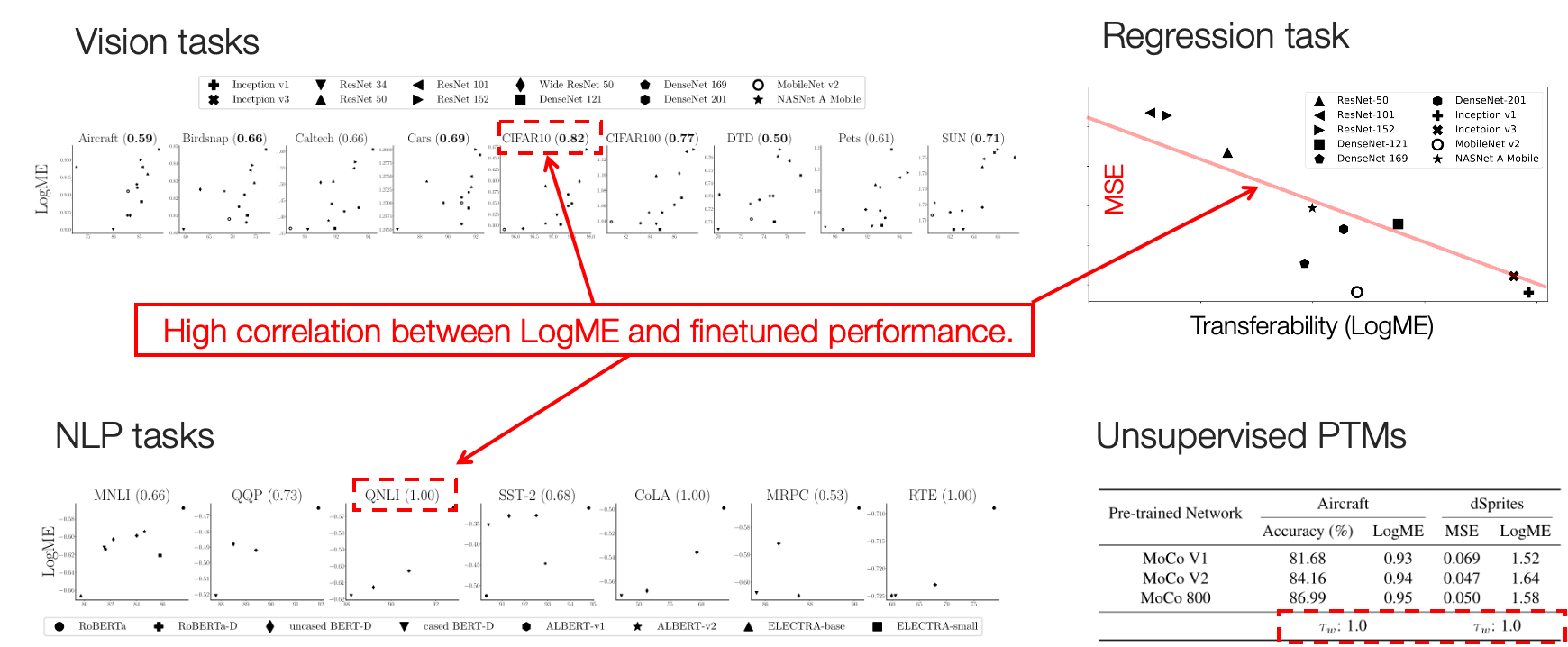
Good metrics should correlate well with fine-tuned performance.
Selecting Pre-trained Models
With a transferability ranking, a straightforward action is to use the best ranked model. This is true for most academic researchers as they are not constrained by the inference cost of deployed models. However, in a practical usage scenario, there are often constraints on the network architecture, parameter count, or FLOPs of computation. Therefore, the pre-trained model
Tuning Pre-trained Models
The difficulty of transferring knowledge from top-K models
To confirm the effectiveness of the proposed "ranking and tuning" paradigm, we conduct experiments on some popular tasks like fine-grained Aircraft classification and bird classification. The red-dashed line is the accuracy of picking the most popular pre-trained model, which is shown to be sub-optimal. By first ranking and then tuning top-K models, we can improve the accuracy by 3%~5%, thanks to the diversity of the model hub.
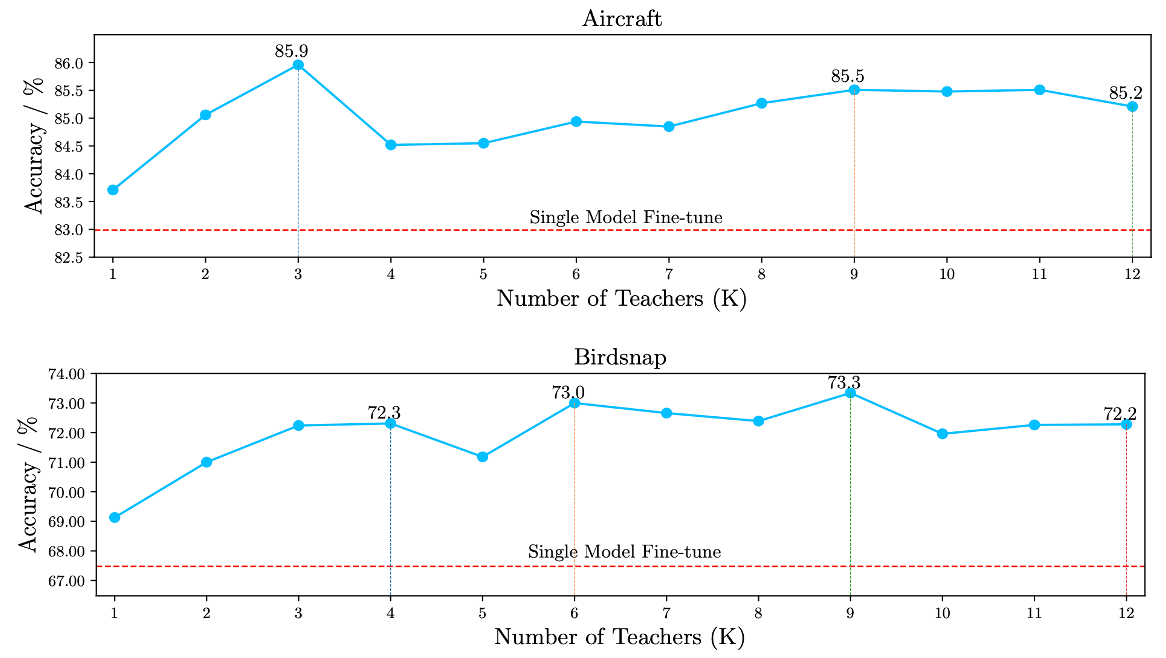
Effectiveness of the proposed "ranking and tuning" paradigm.
Concluding remarks
Pre-trained models are universally acknowledged as a foundation of deep learning. Researchers have explored many ways to create and exploit pre-trained models, but little is done for exploiting model hubs. Our paper [2] takes the first step to show the value of exploiting all models in the model hub. The paradigm can be attractive for practitioners.
To take a step further, the scope of pre-trained model hub is not limited to large models: AI companies usually re-train models every once in a while, and all the models trained in the past can be treated as a model hub. It is a reckless waste to just discard those models. These models can be exploited to improve performance, or at least accelerate training of new models using the proposed "ranking and tuning" paradigm.
Trained models are assets, and how to activate their potential is an important problem. I believe the paper [2] is just a starting point and there is still a long way to fully addrss the problem.
References
[1] Kaplan et al., Scaling Laws for Neural Language Models, Arxiv 2020
[2] You et al., Ranking and Tuning Pre-trained Models: A New Paradigm for Exploiting Model Hubs, JMLR 2022
[3] Nguyen et al., LEEP: A New Measure to Evaluate Transferability of Learned Representations, ICML 2020
[4] You et al., LogME: Practical Assessment of Pre-trained Models for Transfer Learning, ICML 2021
[5] Ding et al., PACTran: PAC-Bayesian Metrics for Estimating the Transferability of Pretrained Models to Classification Tasks, ECCV 2022
[6] Pandy et al., Transferability Estimation using Bhattacharyya Class Separability, CVPR 2022
Recommended for you
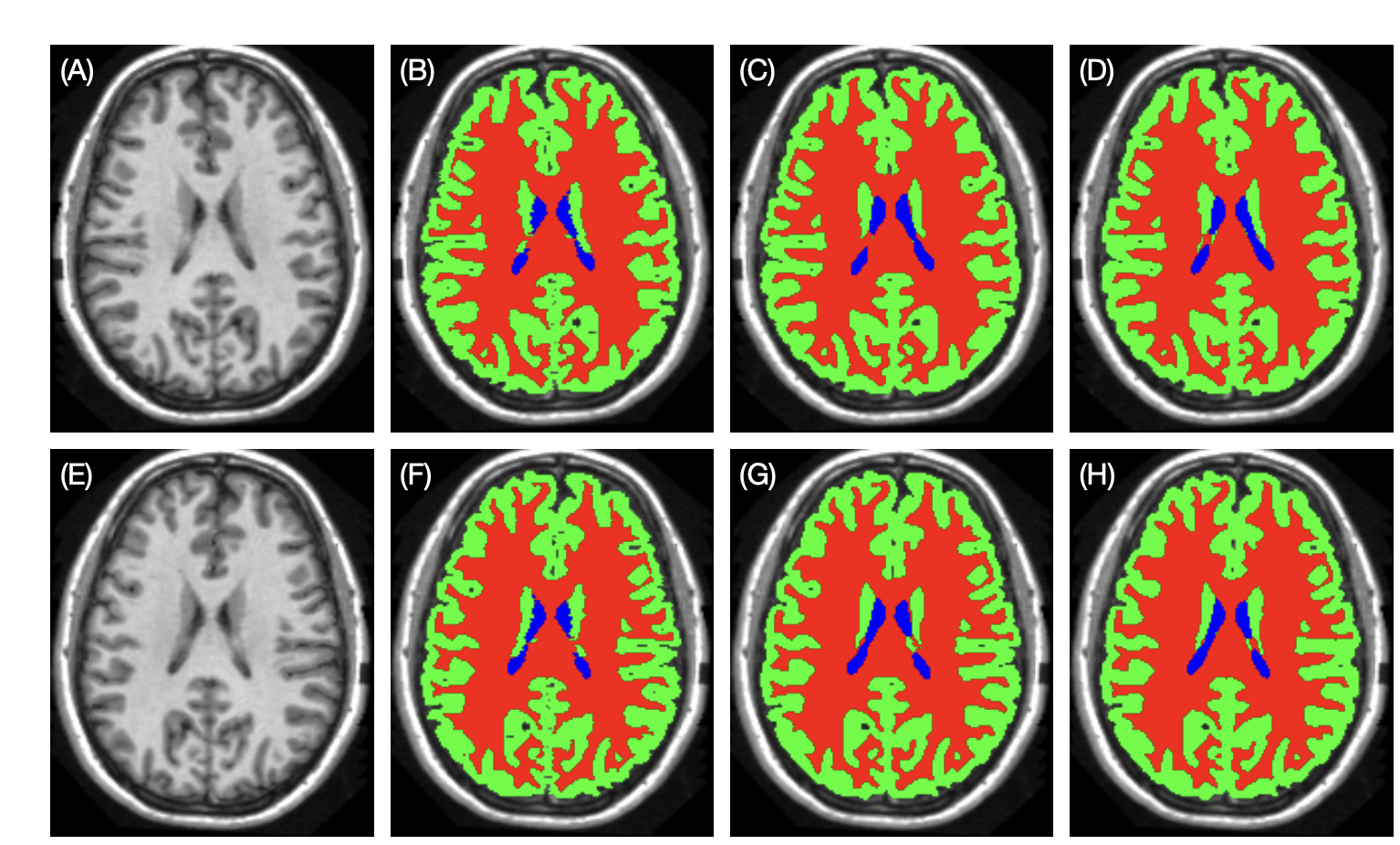
Group Equivariant Convolutional Networks in Medical Image Analysis
Group Equivariant Convolutional Networks in Medical Image Analysis
This is a brief review of G-CNNs' applications in medical image analysis, including fundamental knowledge of group equivariant convolutional networks, and applications in medical images' classification and segmentation.