A Review of Trustworthy Graph Learning
1. Introduction
Graph machine learning, graph neural networks, in particular, have attracted considerable attention. There has been an exponential growth of research on graph neural networks (GNNs) in the path few years, ranging from finance and e-commerce, to physics, biomedical science, and computational chemistry[1][2]. The increasing number of works on GNNs indicates a global trend in both academic and industrial communities. So far, GNNs are becoming the frontier of deep learning.
While most active research on GNNs focuses on developing accurate models, there are concerns raised by communities. One major concern is whether current GNNs are trustworthy. Such concern is inevitable when GNNs step into real-world applications, especially in risk-sensitive and security-critical domains. Their increasing deployment in upcoming applications such as autonomous driving, automated financial loan approval, and drug discovery have many worrying about the level of trustworthiness associated with GNNs[3]. Unfortunately, many weaker sides of current GNNs have been exposed through adversarial attacks, bias, and lack of explainability in the literature[4]. Therefore, there is a pressing demand in studying the trustworthiness of GNNs.
What does Trustworthy Mean? Trustworthy is a term used to describe a model that is lawful, ethically adherent, and technically robust. It is based on the idea that the model will reach its full potential when trust can be established in each stage of its lifecycle, from design to development, deployment, and use. Unless stated, we focus on the design and development of a trustworthy GNN model in this review.
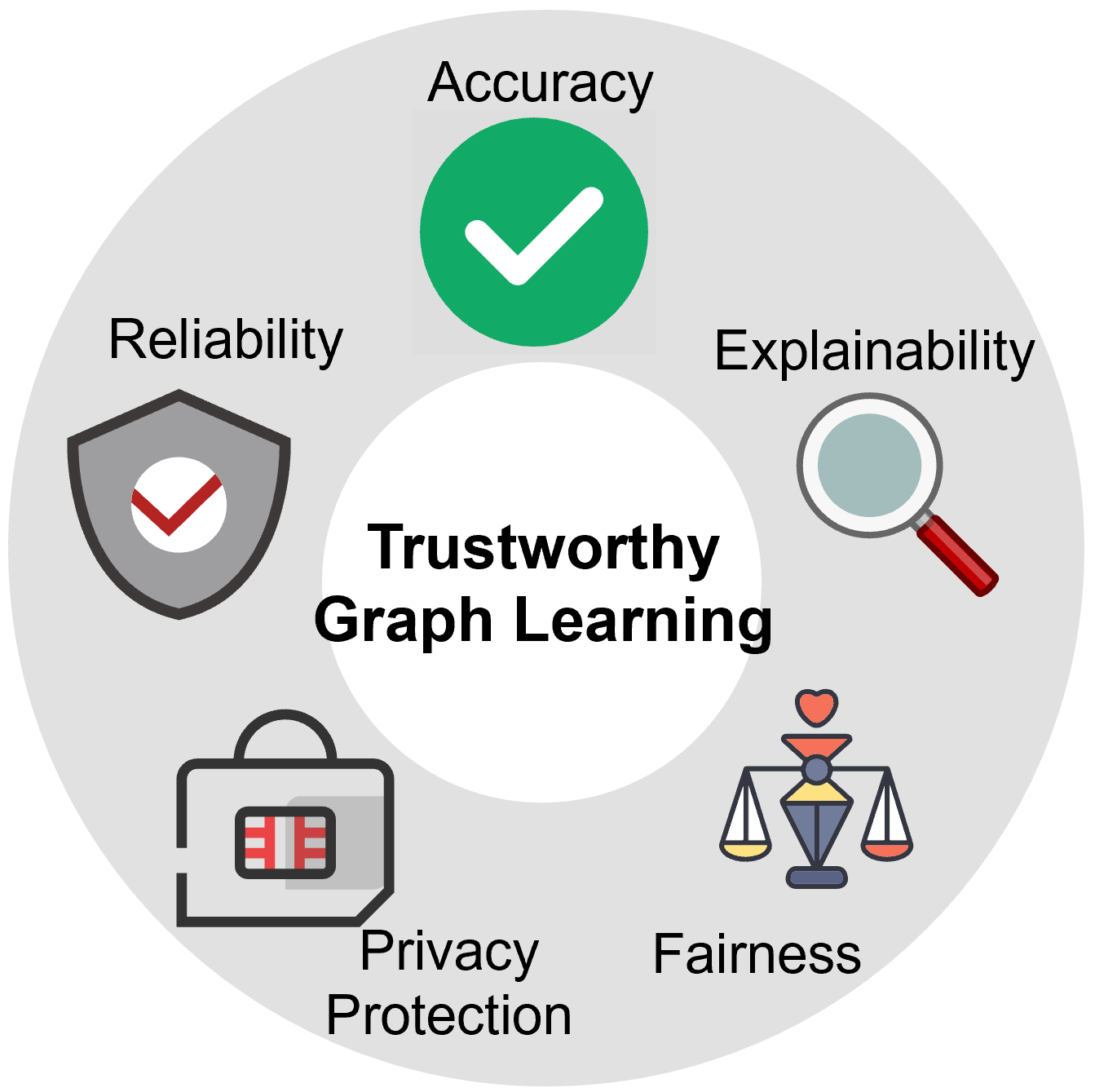
How to Achieve Trustworthiness? Broadly speaking, a trustworthy GNN model involves various aspects, including but not limited to accuracy, robustness, explainability, algorithmic fairness, and also privacy protection, as shown in Figure 1. Basically, a trustworthy GNN is expected to generate accurate output, consistent with the ground truth, as much as possible. In addition, it should be resilient and secure. Moreover, the model itself must allow explainable for the prediction, which can help humans to make a decision with higher confidence. One step further, a trustworthy GNN should ensure full privacy of the users as well as data privacy. Last but not least, it should be fair, unbiased, and accessible to all groups.
There are some efforts in developing trustworthy GNNs in the literature. However, they mainly focus on a single aspect of GNNs (e.g., robustness), while ignoring other aspects of trustworthiness. Typically, greedily pursuing any single aspect alone does not necessarily result in an optimal solution towards more trustworthy GNNs. In this review, we will explore how to develop trustworthy GNN models from different aspects. Our goal is to provide a brief overview on the advanced research of trustworthy graph learning and discuss possible directions in the underlying areas. This review is organized as follows: we first introduce the reliability of GNNs against three threats and the corresponding solutions. Then, we subsequently discuss the explainability, privacy protection, and fairness of GNNs. Finally, we draw our conclusion and point out future directions in the area of trustworthy graph learning.

2. Reliability of Graph Neural Networks
Despite the progress made by GNNs in recent years, they have been exposed through different reliability threats in the current rapidly evolving works. Reliability is an important aspect of a trustworthy GNN model, which refers to the consistency of results across different inputs that might be dynamically changed or perturbed[5][6][7][8][9][10][11][12][13]. According to our recent review[13:1], the reliability of GNNs involves three aspects of threats that are faced in real-world applications: inherent noise, distribution shift, and adversarial attacks. Specifically, inherent noise refers to any random fluctuations of data that are irreducible and hinders the learning of a model. Distribution shift refers to a mismatch between the training and testing distributions. Adversarial attack is a manipulation of human action on the input data that aims to cause the model to make a mistake.
As illustrated in Figure 2, the three above threats occur throughout a typical pipeline of graph learning. Typically, inherent noise and distribution shift are inevitable and unintentionally introduced during data generation, which may be attributed to the limited knowledge of data or sampling/environment bias. On the other hand, adversarial attack is intentionally designed by malicious attackers or fraudsters after data generation (particularly before model training or testing) to mislead the target models.
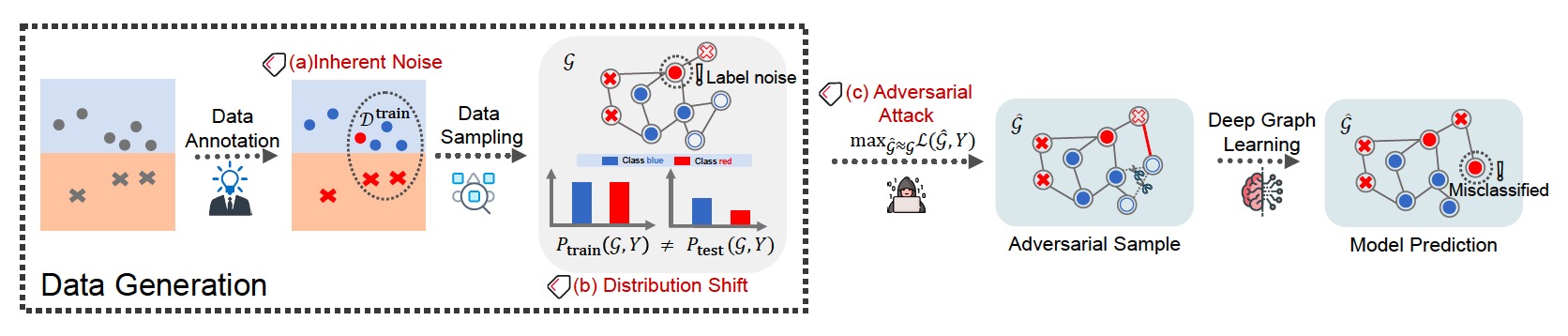 Figure 2: An illustrative example on deep graph learning against (a) inherent noise, (b) distribution shift, and (c) adversarial attack. Image from Wu et al.[13:2] .
Figure 2: An illustrative example on deep graph learning against (a) inherent noise, (b) distribution shift, and (c) adversarial attack. Image from Wu et al.[13:2] .2.1. Reliability threats of Graph Neural Networks
We further give the description of different reliability threats of GNNs as follows:
Inherent Noise is commonly existed in real-world graph data and unavoidable for graph learning. According to the different types of noise, we categorize inherent noise into structure noise, attribute noise, and label noise:
where
Distribution Shift refers to a mismatch between the training and testing distributions, which is also a common challenge for machine learning:
where
Adversarial Attack is a new threat addressed on the deep graph learning models, which aims to cause a model to make mistakes with carefully-crafted unnoticeable perturbations (adversarial examples) or predefined patterns (backdoor triggers):
where
2.2. Techinques against Reliability Threats
The adversarial reliability of GNNs is highly desired for many real-world systems. To improve the robustness or reliability of GNNs against such threats, extensive efforts were made during the past few years. Technically, we divide these methods into three categories according to different learning stages of GNNs: graph processing, model robustification, and robust training.
Graph Processing. From data perspective, a natural idea is to process the input graph to remove adversarial perturbations or noise thus mitigating its negative effects. In this regard, the task-irrelevant edges/nodes can be detected and pruned before training based on empirical observations, such as homogeneity. For example, the adversarially perturbed or noise nodes have low similarity to some of their neighbors, which can thus be pruned before training/testing.
Model Robustification. Refining the model to prepare itself against potential reliability threats is another promising solution. Specifically, the robustification of GNNs can be achieved by improving the model architecture or aggregation scheme. For example, employing regularizations or constraints on the model itself to improve the architecture or deriving a robust aggregation function to improve the aggregation scheme.
Robust Training. Graph robust training proposes to enhance the model robustness against different threats such as distribution shift or adversarial attacks. In this regard, adversarial training is a widely used practical solution to resist adversarial attacks, which builds models on a training set augmented with handcrafted adversarial samples. Furthermore, adversarial training can also help the model generalize to out-of-distribution (OOD) samples by making it invariant to small fluctuations in input data.
3. Explainbility of Graph Neural Networks
An explainable model must explain its behavior so the users understand why certain predictions are made by the model. In the past few years, the explainability of deep learning models on images and texts has achieved significant progress. In the area of graph data, however, the explainability of GNNs is far less explored, which makes GNNs suffer from the black-box problem and limits their adoption in real-world applications[14][15]. The explainability of GNNs is critical for understanding the mechanism underlying them and improving their trustworthiness. Hence, it is imperative to develop explanation techniques for the improved transparency of GNNs.
Recently, several methods are proposed to study the underlying relationships behind the predictions of GNNs. Generally, they seek to analyze the sensitivity of GNNs w.r.t. the inputs, such as nodes, edges, and sub-graphs which are crucial for the model predictions. These methods are input-dependent and are sensitive to different input graphs. Meanwhile, several works are proposed to provide input-independent explanations by studying what input graph patterns can lead to a certain GNN behavior or the intrinsic mechanism of hidden neurons. In this section, different methods are categorized into two categories: post-hoc methods and self-explainable methods, based on whether the explanation method is architecturally built-in within the graph model.
3.1. Post-hoc Methods
Given a pre-trained graph model, the post-hoc methods focus on discovering the crucial substructures that most influence the prediction (see Figure 3)[16]. Based on the knowledge of the explanation methods, we further categorize the post-hoc methods into the white-box methods and the black-box methods. The white-box methods, such as the decomposition-based methods and the gradient-based methods, have access to the model parameters or gradients. Specifically, the decomposition-based methods decompose the prediction into the contributions of different input substructures, and the gradient-based methods generally employ the output-gradient or logits-gradient w.r.t the input graph to identify the importance of the input portions. Unlike the white-box methods, the black-box methods assume no knowledge of GNN's parameters or gradients and only require the input and the output of the graph model. For example, the surrogate-based methods leverage a simple and explainable model to fit the output space of the complex graph model. Moreover, the generation-based methods either use generative models to synthesize the crucial patterns customized for input or generate key structures to globally explain the behavior of model predictions. In addition, the perturbation-based methods generally remove the unimportant edges and nodes so that the final prediction remains unchanged under such perturbations. In the contrast, the counterfactual-based methods identify the minimal substructure of the input which would change the original prediction if removed.
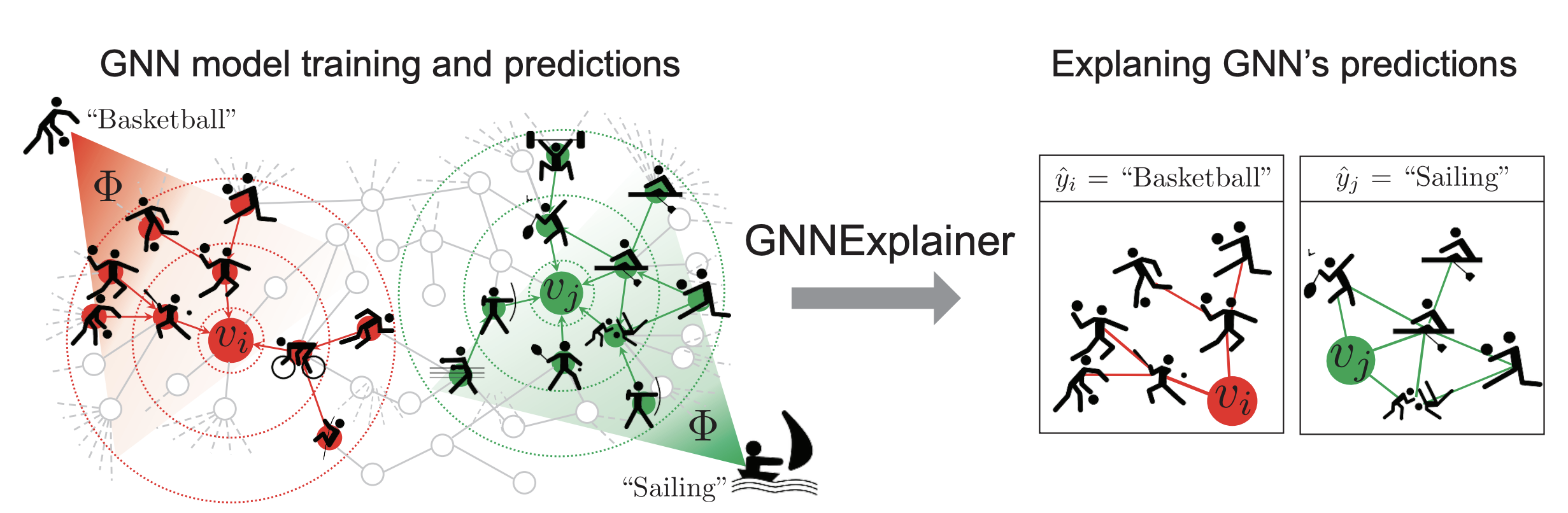 Figure 3: GNNEXPLAINER[16:1] provides interpretable explanations for predictions made by any GNN model on any graph-based machine learning task.. Image from Ying et al.[16:2].
Figure 3: GNNEXPLAINER[16:1] provides interpretable explanations for predictions made by any GNN model on any graph-based machine learning task.. Image from Ying et al.[16:2].3.2. Self-explainable Methods
Apart from the post-hoc explanation methods, the self-explainable methods have attracted increasing attention in the recent literature. These methods embed the intrinsic explanations in the architectures of the GNN models and simultaneously make predictions and generate the corresponding explanations during the inference time. Generally, they either recognize the predictive substructures of the input graph for the explanation or induce the evidence of the outputs via regularization. Compared with the post-hoc explanation methods, the self-explainable methods enjoy computationally and time efficiency by simultaneously making predictions and producing the corresponding explanations. However, it also requires domain knowledge to design the built-in module for the intrinsic explanations.
4. Privacy Protection of Graph Neural Networks
The recent successes of graph learning are typically built upon large-scale graph data. However, GNNs still face many problems and one of them is the data silos. In practice, graph data are always distributed to different organizations and cannot be shared due to privacy concerns or commercial competition. Here we take e-commerce recommendation systems building as an example. In this case, all users and items can form a large bipartite graph wherein a node denotes a used or an item, and a link indicates whether a user is interested in a specific item. The users' features are typically distributed over different organizations. For example, the deposit and loans of a user are always stored in a financial organization (e.g., PayPal) while the shopping history is always stored in the e-commerce organizations (e.g., Amazon). If we further take the social connections between users into consideration, this data is always stored in social network departments such as Facebook. As we can see from the above example, the user-item graph is demonstrated as a large heterogeneous graph wherein the link and node data is held by different organizations or departments, i.e, "data isolated island". This issue presents serious challenges for applying GNNs to real-world scenarios.
To solve this issue, numerous efforts have been made to build privacy-preserving graph learning which aims to build a graph learning framework while protecting data or model privacy. In this review, we categorize previous research work of privacy protection into three directions, namely, federated graph learning, privacy inference attack, and private graph learning. Specifically, federated graph learning aims to provide a general distributed learning paradigm enabling multiple organizations to jointly train a global model without sharing their own raw data. While federated graph learning has provided protection for raw data, most work still needs to share intermediate data such as gradients or hidden features between clients, and these data can also contain some sensitive information. This information can be reconstructed by some specific privacy inference attacks which is the second part of this section. Further, we review some recent private graph learning work that aims to employ cryptographic techniques to prevent the above attacks.
4.1. Federated Graph Learning
Federated Graph learning (FGL) is a distributed collaborative machine learning setting where clients can collaboratively train a shared model under the orchestration of a central server while keeping the data decentralized[17]. As shown in Figure 4, different graphs are distributed to different clients, where each client performs graph-level learning locally to train a global GNN. In contrast to traditional federated learning, there are connections among graphs in different clients, i.e., the Non-IID property of graph data, giving rise to challenges in centrally training GNNs[18].
 Figure 4: A typical framework of federated graph learning. Image from Zhang et al.[17:1].
Figure 4: A typical framework of federated graph learning. Image from Zhang et al.[17:1].A simple way to train the GNNs in the federated leaning setting is to apply FedAvg on the objection function:
where
4.2. Privacy Inference Attack
As introduced in Section 2, GNNs are vulnerable to adversarial attacks that aim to mislead the prediction of a model. Recent literature has also revealed two major categories of privacy threats in graph learning techniques. The inference attack is a data mining technique performed by analyzing data in order to illegitimately gain knowledge about a subject or database[19][20][21]. According to different levels of adversarial behaviors, we can categorize inference attacks into two categories, i.e., membership inference attack (MIA) and model extraction attack (MEA). Both threats happen in the test phase of a trained model to reveal secret information.
Membership Inference Attack (MIA). As shown in Figure 5, in MIA, an adversary is given the target element (e.g., the nodes, edges), information about the training graph (e.g., local topology), intermediate outputs of the victim model (e.g., node embeddings), and black/white-box access to the victim model[22].
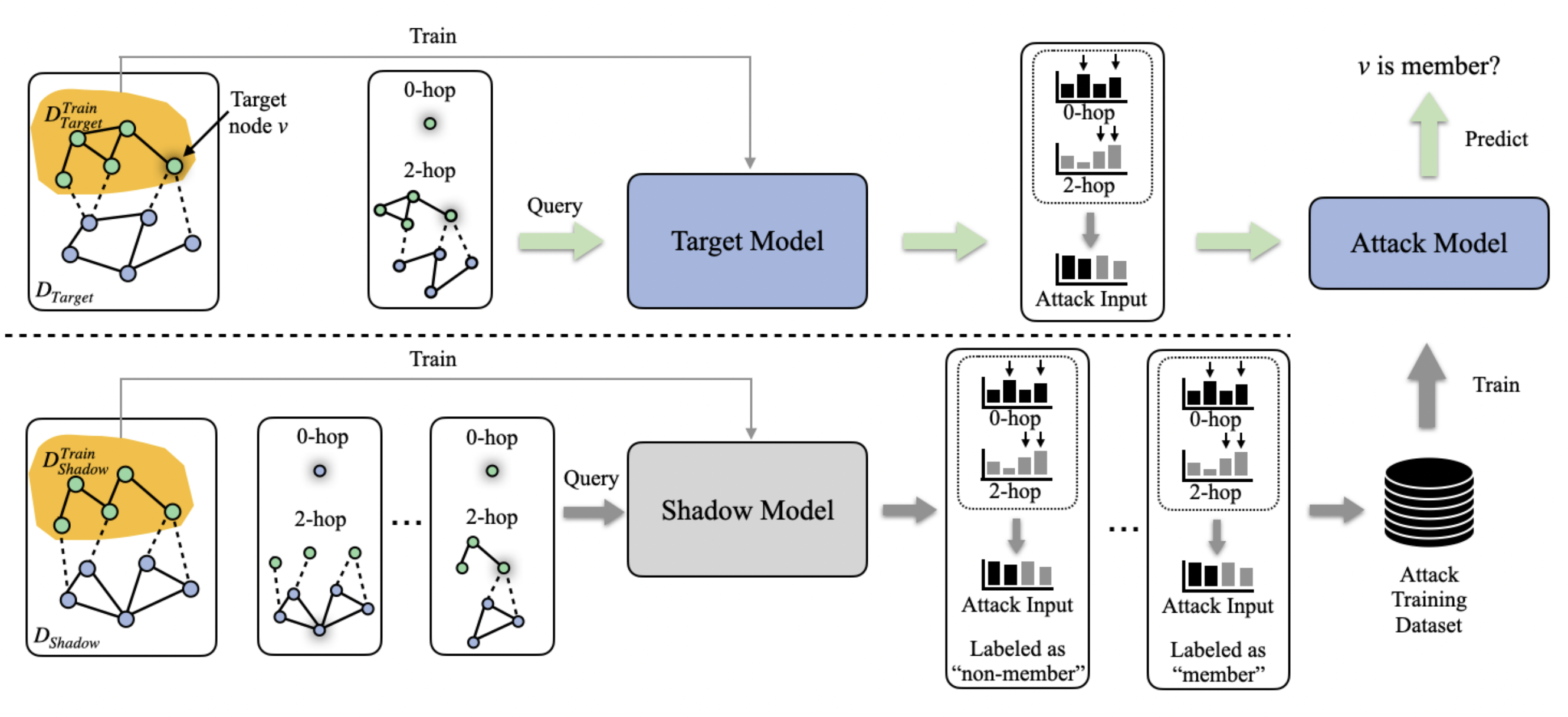 Figure 5: A illustrative example of membership inference attacks on GNNs. Image from He et al.[22:1].
Figure 5: A illustrative example of membership inference attacks on GNNs. Image from He et al.[22:1].Model Extraction Attack (MEA). Apart from the data-level privacy threat, graph learning models are also vulnerable to model-level threats, i.e., model extractions attacks (MEA). As shown in Figure 6, MEA aims to reconstruct a substitute model from the responses of generated queries to the target model[23].
 Figure 6: An illustrative example of model extraction attacks on GNNs. Image from Wu et al.[23:1].
Figure 6: An illustrative example of model extraction attacks on GNNs. Image from Wu et al.[23:1].4.3. Private Graph Learning
Although several federated graph learning methods have been studied to preserve the privacy of learning models and training data, there are more privacy issues to be addressed. For example, the leak of gradient or hidden embedding during federated learning may cause kinds of attacks, e.g., model inversion attacks on GNN models. To this end, existing work has proposed different solutions for private graph learning. Technically, we divide them into two types, i.e., differential privacy (DP) and secure multi-party computation (MPC) based methods.
Differential Privacy (DP). DP is the most common notion of privacy for algorithms on statistical databases, which bounds the change in output distribution of a mechanism when there is a small change in its input. Typically, we have
Multi-party Computation (MPC). MPC is a cryptographic tool that allows multiple parties to make calculations using their combined data, without revealing their individual input. In this regard, MPC can be adopted as an efficient tool to build provable-secure GNNs.
DP-based private graph learning has high efficiency, however, there is a trade-off between privacy and utility. In contrast, MPC-based private graph learning can achieve comparable performance with plaintext graph learning models, but it often comes with a serious efficiency cost.
5. Fairness of Graph Neural Networks
Recent studies have revealed that GNNs also show human-like discriminatory bias or make unfair decisions. In other words, GNNs may make predictions based on protected sensitive attributes, e.g., skin color and gender, which also results in privacy protection issues. For example, a job recommendation system built on GNNs would promote more employment opportunities to male candidates than to females if models are trained to reflect the distribution of the training data which often contains historical bias and discrimination[24]. On the other hand, GNNs are also unfair to different groups of data. As shown in Figure 7, an accurate GNN may not always be fair to males and females. In this regard, some groups of nodes are more vulnerable to adversarial attacks than other groups, posing reliability issues in a graph[25]. Therefore, the fairness of GNNs is also closely related to other aspects of the trustworthiness of GNNs.
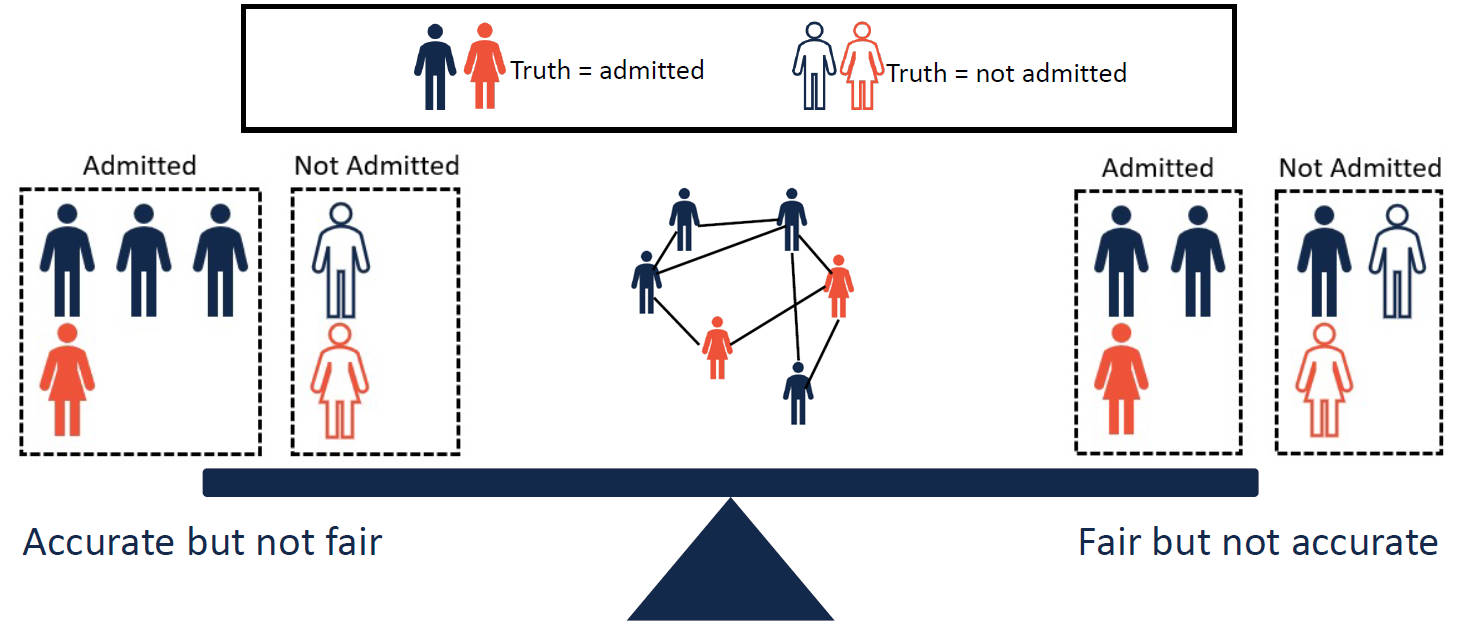 Figure 7: Trade-off between model utility and fairness.
Figure 7: Trade-off between model utility and fairness.Compared with other deep learning models, it seems that the unfairness or bias in GNNs is more evident. This is in part due to the message passing mechanism of GNNs, i.e., propagating information from neighborhoods of nodes based on the graph structure. Therefore, the discrimination or bias in GNNs is more significant as they can be further magnified by graph structures and the message passing mechanism.
There are several attempts to evaluate the fairness of GNNs, where the most frequently used metric is statistical parity:
Statistical Parity is a measure that whether the predictions are independent with the sensitive attributes
where
Many works have been conducted to mitigate the bias in the training data to achieve fairness in graph learning. Based on which stage of the machine learning training process is revised, algorithms could be split into three categories: the pre-processing approaches, the in-processing approaches, and the post-processing approaches.
Pre-processing Approaches are model-agnostic as they are applied before training GNNs. By treating the bias in the graph data as a kind of noise, these approaches are proposed to modify the training data through correcting labels, revising attributes of data, generating unbiased labeled data, to obtain fair representations.
In-processing Approaches are applied in the training phases to revise the models, which imposes additional regularization terms or a new objective function. For example, adversarial training with perturbations on the biased groups is a natural idea to ensure the fairness of GNNs.
Post-processing Approaches are designed to directly change the predictions of GNNs to ensure fairness. In this regard, different calibration methods are adopted to debias the model.
6. Conclusion and Future Direction
In this review, we briefly introduce different aspects of trustworthy graph learning, focusing on the reliability, explainability, privacy protection, and fairness of GNNs. As trustworthy graph learning is still a relatively new area, there are still a lot of challenges. We suggest four future research directions as follows.
Problem Definition. The trustworthiness of GNNs is still an open question for the entire community. We still need a proper and well-accepted definition of the trustworthiness of GNNs in the graph domain. A clearer definition can also benefit the research in this area.
Theoretical Framework. Despite the advances in trustworthy learning, there is still a lack of a theoretical framework to analyze the effectiveness of these works from a unified perspective. In addition, a theoretical framework can help better understand the mechanism of GNNs and achieve trustworthiness.
Evaluation Metric. It is difficult to evaluate whether a GNN is trustworthy as the graph data is difficult to visualize and understand by human experts like images and texts. In this regard, a better quantitative evaluation metric is required for better assessing the trustworthiness of GNNs.
Connection Among Different Aspects. It is clear that different aspects of trustworthiness are closely related. For example, the study of privacy on graphs is also directly to fairness on graphs due to the natural overlaps between privacy and fairness. In addition, the topic of explainability is also directly related to in aid of debugging GNNs models and uncovering biased decision-making. So far, there have been few efforts to understand and explore their relationships. In the future, we hope the study could combine different aspects of research to achieve better trustworthiness of GNNs.
7. References
- Zhou, Yu, et al. "Graph Neural Networks: Taxonomy, Advances, and Trends." ACM Transactions on Intelligent Systems and Technology (TIST) 13.1 (2022): 1-54. ↩︎
- Waikhom, Lilapati, and Ripon Patgiri. "Graph Neural Networks: Methods, Applications, and Opportunities." arXiv preprint arXiv:2108.10733 (2021). ↩︎
- Li, Bo, et al. "Trustworthy AI: From Principles to Practices." arXiv preprint arXiv:2110.01167 (2021). ↩︎
- Liu, Haochen, et al. "Trustworthy ai: A computational perspective." arXiv preprint arXiv:2107.06641 (2021). ↩︎
- Zhu, Yanqiao, et al. "Deep graph structure learning for robust representations: A survey." arXiv preprint arXiv:2103.03036 (2021). ↩︎
- Xu, Han, et al. "Adversarial attacks and defenses in images, graphs and text: A review." International Journal of Automation and Computing 17.2 (2020): 151-178. ↩︎
- Zhang, Ziwei, Peng Cui, and Wenwu Zhu. "Deep learning on graphs: A survey." IEEE Transactions on Knowledge and Data Engineering (2020). ↩︎
- Sun, Lichao, et al. "Adversarial attack and defense on graph data: A survey." arXiv preprint arXiv:1812.10528 (2018). ↩︎
- Chen, Liang, et al. "A survey of adversarial learning on graphs." arXiv preprint arXiv:2003.05730 (2020). ↩︎
- Xu, Jiarong, et al. "Robustness of deep learning models on graphs: A survey." AI Open 2 (2021): 69-78. ↩︎
- Zhang, Zeyu, and Yulong Pei. "A Comparative Study on Robust Graph Neural Networks to Structural Noises." arXiv preprint arXiv:2112.06070 (2021). ↩︎
- Jin, Wei, et al. "Adversarial Attacks and Defenses on Graphs: A Review, A Tool and Empirical Studies." arXiv preprint arXiv:2003.00653 (2020). ↩︎
- Yuan, Hao, et al. "Explainability in graph neural networks: A taxonomic survey." arXiv preprint arXiv:2012.15445 (2020). ↩︎
- Li, Peibo, et al. "Explainability in Graph Neural Networks: An Experimental Survey." arXiv preprint arXiv:2203.09258 (2022). ↩︎
- Liu, Rui, and Han Yu. "Federated Graph Neural Networks: Overview, Techniques and Challenges." arXiv preprint arXiv:2202.07256 (2022). ↩︎
- Casas-Roma, Jordi, Jordi Herrera-Joancomartí, and Vicenç Torra. "A survey of graph-modification techniques for privacy-preserving on networks." Artificial Intelligence Review 47.3 (2017): 341-366. ↩︎
- Zheleva, Elena, and Lise Getoor. "Preserving the privacy of sensitive relationships in graph data." International workshop on privacy, security, and trust in KDD. Springer, Berlin, Heidelberg, 2007. ↩︎
- Li, Kaiyang, et al. "Adversarial privacy-preserving graph embedding against inference attack." IEEE Internet of Things Journal 8.8 (2020): 6904-6915. ↩︎
- Zhang, Wenbin, et al. "Fairness Amidst Non-IID Graph Data: A Literature Review." arXiv preprint arXiv:2202.07170 (2022). ↩︎
- Dai, Enyan, and Suhang Wang. "Say no to the discrimination: Learning fair graph neural networks with limited sensitive attribute information." Proceedings of the 14th ACM International Conference on Web Search and Data Mining. 2021. ↩︎