Widely anticipated to be the harbinger of the next technological revolution, quantum computation (and quantum technology more broadly) has entrenched itself as a major research focus in the physics community.

Such fanfare has not appeared from nowhere; theoretical proposals for quantum algorithms which suggest accelerations in seemingly intractable chemistry, cryptography, and even financial problems continue to emerge as the field blossoms ^[1][2][3]. Another community which hopes that a quantum computational dawn will speed up their algorithms is that of deep learning, so much so that the subfield quantum machine learning has grown into a research area of its own^[4]. Unfortunately, current-day quantum devices are of a quality significantly below that required to execute any of the algorithms alluded to above, for a wide range of reasons. So, the potential for technological symbiosis presents itself: in this era where quantum computers are too immature to meaningfully assist the development of deep learning algorithms, can deep learning be used to help fix the enduring problems of quantum computation?

Quantum control has proven to be a fertile breeding ground for this intersection of research. To understand why, it is beneficial to first appreciate the power of quantum information.

The fundamental difference between classical and quantum information can be explained relatively easily. A classical bit (one unit of classical information) can occupy one of two basis states; 0 or 1. In contrast, a quantum bit (one unit of quantum information) can live in some combination of these basis states (what is called a complex superposition). Simply, a unit of quantum information has a broader zoo of states which it can occupy during a computation.

In addition to this larger state space for an individual quantum bit, there exist unique multi-bit states which can be occupied by pairs or hordes of quantum bits. The phenomenom of quantum bits joining forces to form inseperable larger quantum states is called quantum entanglement.

Broadly speaking, the expanded array of states which can be occupied by functional quantum computing chips allow theoreticians to develop novel algorithms which crunch information in a more efficient way, as compared to computing schemes which can't harness these behaviours.

There are a myriad of proposals for how to build a quantum chip, consisting of functional quantum bits which can exist in stable superposition and entangle with each other. In any of these proposed architectures, a method for precise control of the quantum state is required to perform computation. This control enables the user to reliably and robustly guide an array of quantum bits from one quantum state to another, with error rates below some threshold that external error correction techniques can handle. To crystallise this idea, we briefly touch on the control mechanism for a specific architecture of quantum computing, the superconducting quantum computer.

Electrical circuits fabricated from superconducting materials behave according to the laws of quantum mechanics, when cooled to cryogenic temperatures. It is this premise which facilitates superconducting quantum computers, which essentially boil down to meticulously designed electrical circuits acting as individual quantum bits. These circuits are specially designed such that electromagnetic pulses within the microwave frequency range interact strongly with them, and can be used to meaningfully evolve their quantum state.

In short, the control mechanism for a classical bit can be as simple as sending an electrical signal to encode 1 or not sending an electrical signal to encode 0. For a superconducting quantum bit, one has to shape a microwave pulse in order to guide the quantum state through the zoo of possible candidates to the goal state. An example of such a pulse design is seen below; two separate pulses, offset by a phase of ${90}^{\mathrm{o}}$${90}^{\mathrm{o}}$90^(o)90^\mathrm{o}, are shown in blue and orange. These are summed to create an overall shape which optimally performs the desired state evolution.

Regardless of the quantum computing architecture in question, the control mechanism used to traverse the landscape of quantum states is conventionally in the form of a shaped pulse. In general, for a complex system, there exists no analytical method to determine what this pulse shape should be. The question of optimal pulse design for control of quantum systems has therefore spurred significant research throughout the development lifespan of quantum computation.

It is no coincidence now that we segue from the topic of an unsolved optimisation problem into a brief introduction to reinforcement learning.

The reinforcement learning (RL) training scheme is a reward-based Markovian process: an agent takes some action in some environment, and this action updates the state of the environment and returns some corresponding reward.

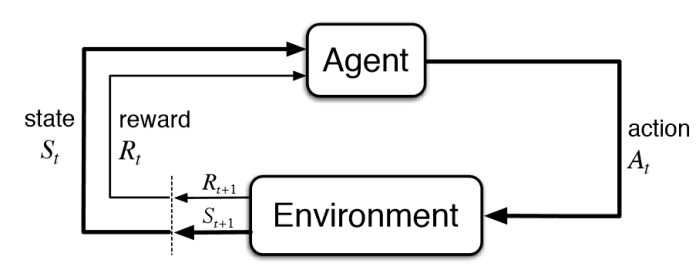
In the case of deep RL, the policy which the agent follows is parametrised by a deep neural network, which takes an observation of the environment state as an input, processes this output through arbitrary neuron layers, returns some action as an output, and repeats the process, all the while working to maximise the cumulative reward it will receive.

RL has enjoyed its most celebrated successes in the gaming and robotics domains, but applications to the physical sciences certainly exist. In 2021 alone, RL was used to make notable progress on high-dimensional and non-linear problems such as control of optics systems in astronomy, rare trajectory sampling and fluid mechanics^[5][6][7]. Quantum technology provides a space with remarkably high dimensionality and non-linearity, and the adoption of deep RL in particular has accordingly been highest within this field.

The efforts to marry RL to the unsolved problem of optimal quantum control came to fruition with a series of publications throughout 2018 and early 2019 documenting various successes in the field^{[8][9][10][11]}. These methods were often centred around tabular Q-learning approaches, which were able to produce results comparable to existing optimal control algorithms.

A breakthrough study from the University of Hong Kong directly compared standard and deep reinforcement learning methods to existing gradient descent methods for the problem of quantum control^[12]. DRL demonstrated advantage in two key situations; when the parameters used to define the control pulse were discretised, and when the number of quantum bits is scaled up. The second finding is particularly promising for DRL; a significant scale-up in the number of quantum bits on-chip is a necessity for the implementation of useful quantum algorithms. The flexibility of RL methods also offered an advantage in adaptive segmentation, or finding a pulse which performed the state preparation with high accuracy in a shorter amount of time. The figure below demonstrates DRL (embodied by deep Q-learning DQL and policy gradient PG) demonstrating advantage in the metric of pulse quality (F) as the number of quantum bits (spins) increase.

This finding is fortified by concurrent 2019 research which deployed a DRL algorithm to generate novel pulse designs, outperforming the state-of-the-art techniques at the time for a particular state evolution in the quantum dot field^[13]. The DRL algorithm excelled in an environment significantly more complex than that encountered in previous research, as it dealt with loss of quantum information through decay and dephasing which mimics real quantum hardware. Furthermore, the control pulses it designed were piece-wise pulses with amplitudes selected from a continuous distribution, a problem domain in which the advantage of DRL had previously not been clear. This evidence that outsourcing a quantum control task to a DRL agent with no prior knowledge of the system could outperform a pulse ansatz developed through years of experimental experience stands as a clear motivation for practitioners in the field to consider DRL as an option in their workflow.

This burgeoning approach proved sufficiently tantalising for the Google Quantum AI group to develop their own approach^[14]. A key distinguisher for this study was a focussed development of the cost function used to train the DRL system, modifying it deliberately in order to create pulse schemes which were more robust to noise sources that commonly disrupt quantum systems. The UFO cost function for quantum control was introduced; mathematically a mouthful, but in essence quite straightforward.

The parameters $\chi ,\beta ,\gamma ,\kappa$$\chi ,\beta ,\gamma ,\kappa$chi,beta,gamma,kappa\chi,\beta,\gamma,\kappa are simply weights which can increase or decrease the impact of terms in the cost function. The first term corresponds to the overall quality of the pulse in performing the task it sets out to do, the second term penalises information leakage from the measurable subspace of the quantum chip, the third penalises boundary condition violation (pulse shape not starting and ending at zero amplitude), and the final term acts to minimise the total runtime of the pulse. With this deliberate and supervised monitoring of pulse quality applied to a cutting-edge DRL algorithm, the Google team is able to generate control pulses with error rates that are two orders of magnitude smaller than those generated by status quo stochastic gradient descent algorithms, given the same computational resources.

Further progress has been made towards the ends of DRL-driven quantum control throughout the last two years^{[15][16][17][18]}, including the first model-free experimental implementation by the Australian company Q-CTRL^[19]. Executed on superconducting quantum processors made publicly available by IBM, a model-free DRL approach is used to successfully enhance default pulse shapes for single-qubit gates (to create arbitrary superposition states) and multi-qubit gates (to create arbitrary entangled states). Focus is placed on the ability of the optimised pulses to demonstrate robustness to parameter drift and noise in the superconducting quantum processors, which can substantially degrade the quality of the default pulses. Achievement of this goal is shown, in part, by the ability of the DRL-generated entangling pulse to maintain higher quality up to 25 days after optimisation, compared to a default entangling pulse applied immediately after optimisation.

As with any growing collaboration between two rapidly advancing fields, DRL for quantum control has some capable research groups making admirable progress. The natural pairing of the problem (control) and methodology (DRL) has been identified and harnessed globally. At present, there remain some clear directions remaining for the subfield to attend to, in order to successfully play a small role in enabling the quantum revolution.

A significant obstacle is that the bulk of DRL control research (and indeed control optimisation in general) occurs in simulation. Quantum systems, with corresponding environmental noise and distortions, are infamously difficult to fully characterise and classically simulate. This means that results developed in simulation have no guarantees to be useful at all in practice. While recent research (per above) seeks to avert this by performing all of its optimisation on quantum hardware, this training can take significant time and resources; it is conceivable that an experimentalist will not be willing to implement these methods and subsequently wait hours for their custom pulse. Further, the nature of quantum measurements restricts the amount of information about pulse quality one can extract from a single experiment. Is there a way to take advantage of the accessibility and power of training algorithms in a classical simulation ('offline') and transfer these learnings to fine-tune pulse designs on the real quantum hardware ('online')?

In addition, quantum algorithms which execute useful tasks involve many gates acting in succession, and therefore many control pulses acting in succession. The quality of a gate can be negatively affected by the gates which have preceded it; errors can propagate in a way which is destructive to the quality of the overall algorithm. This is especially true if the system exhibits non-Markovian noise, when defects in controls which were performed some time ago can return to haunt the efficiency of future pulses. Pulse design with some awareness of the control operations which have preceded them is another area which is yet to be thoroughly explored in the literature.

The fusion of deep reinforcement learning and quantum control will only be a positive endeavour for the future realisation of a universal quantum computer. The literature is brimming with proof-of-concept realisations which function effectively in simulation, and we appear to be embarking on an era where these methods are seeing application in practice. This review seeks to shed some light on this growing intersectional focus, and encourage researchers from not only physics, but also machine learning backgrounds to consider approaching the problem from their perspective. After all, if control advancements prove to be important for successfully accelerating algorithms with a large-scale quantum computer, you might just be helping yourself.